
The work W done by a constant force of magnitude F on a point that moves a displacement s in a straight line in the direction of the force is the productįor example, if a force of 10 newtons ( F = 10 N) acts along a point that travels 2 metres ( s = 2 m), then W = Fs = (10 N) (2 m) = 20 J. Due to work having the same physical dimension as heat, occasionally measurement units typically reserved for heat or energy content, such as therm, BTU and calorie, are used as a measuring unit.

Non-SI units of work include the newton-metre, erg, the foot-pound, the foot-poundal, the kilowatt hour, the litre-atmosphere, and the horsepower-hour. Usage of N⋅m is discouraged by the SI authority, since it can lead to confusion as to whether the quantity expressed in newton-metres is a torque measurement, or a measurement of work. The dimensionally equivalent newton-metre (N⋅m) is sometimes used as the measuring unit for work, but this can be confused with the measurement unit of torque. The SI unit of work is the joule (J), named after the 19th-century English physicist James Prescott Joule, which is defined as the work required to exert a force of one newton through a displacement of one metre.

In 1759, John Smeaton described a quantity that he called "power" "to signify the exertion of strength, gravitation, impulse, or pressure, as to produce motion." Smeaton continues that this quantity can be calculated if "the weight raised is multiplied by the height to which it can be raised in a given time," making this definition remarkably similar to Coriolis'. Īlthough work was not formally used until 1826, similar concepts existed before then. According to Rene Dugas, French engineer and historian, it is to Solomon of Caux "that we owe the term work in the sense that it is used in mechanics now". Etymology Īccording to the 1957 physics textbook by Max Jammer, the term work was introduced in 1826 by the French mathematician Gaspard-Gustave Coriolis as "weight lifted through a height", which is based on the use of early steam engines to lift buckets of water out of flooded ore mines. He was the first to explain that simple machines do not create energy, only transform it. The complete dynamic theory of simple machines was worked out by Italian scientist Galileo Galilei in 1600 in Le Meccaniche ( On Mechanics), in which he showed the underlying mathematical similarity of the machines as force amplifiers. During the Renaissance the dynamics of the Mechanical Powers, as the simple machines were called, began to be studied from the standpoint of how far they could lift a load, in addition to the force they could apply, leading eventually to the new concept of mechanical work. The ancient Greek understanding of physics was limited to the statics of simple machines (the balance of forces), and did not include dynamics or the concept of work.

7.4 Moving in a straight line (skid to a stop).7.3 Derivation for a particle in constrained movement.7.2 General derivation of the work–energy principle for a particle.7.1 Derivation for a particle moving along a straight line.
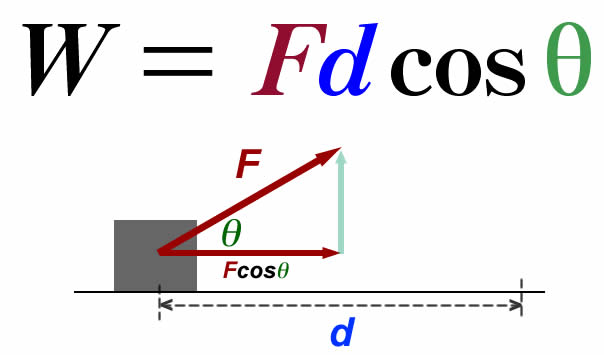
When the force F is constant and the angle between the force and the displacement s is θ, then the work done is given by: If the ball is thrown upwards, the work done by its weight is negative, and is equal to the weight multiplied by the displacement in the upwards direction. įor example, when a ball is held above the ground and then dropped, the work done by the gravitational force on the ball as it falls is positive, and is equal to the weight of the ball (a force) multiplied by the distance to the ground (a displacement). A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force. A force is said to do positive work if when applied it has a component in the direction of the displacement of the point of application. In its simplest form, for a constant force aligned with the direction of motion, it equals the product of the force strength and the distance traveled. In physics, work is the energy transferred to or from an object via the application of force along a displacement.


 0 kommentar(er)
0 kommentar(er)
